原始GAN的优化函数为什么要使用 \(\max \log(D(G(z)))\)
原始GAN的优化目标为:
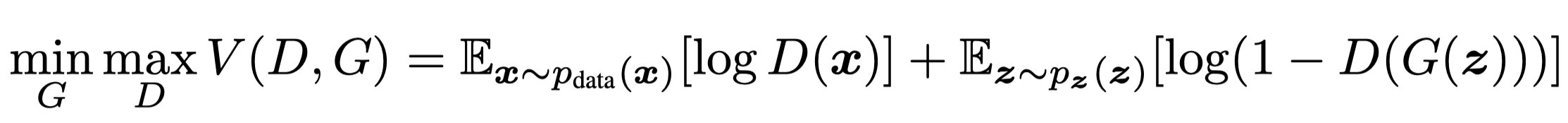
原文中表示在优化G的时候需要重新定义优化目标, 把
换为
In practice, equation 1 may not provide sufficient gradient for G to learn well. Early in learning, when G is poor, D can reject samples with high confidence because they are clearly different from the training data. In this case, log(1 − D(G(z))) saturates. Rather than training G to minimize log(1 − D(G(z))) we can train G to maximize log D(G(z)). This objective function results in the same fixed point of the dynamics of G and D but provides much stronger gradients early in learning.
这段话对初学者来说并不直观, 下面解释一下:
GAN在训练前期时, Discriminator往往要强于Generator, 那么对于fake的输入, Discriminator输出的概率往往接近于0, 相应的logit就接近负无穷, logit对应的梯度非常小, 那么反传到generator时得到的梯度也非常小.
把Discriminator中最后的sigmoid激活函数显式代入到优化目标, 并假设x是\(D(G(z))\)在经过sigmoid得到的 unbouned logit , 那么式(1)变为:
对应图像为:
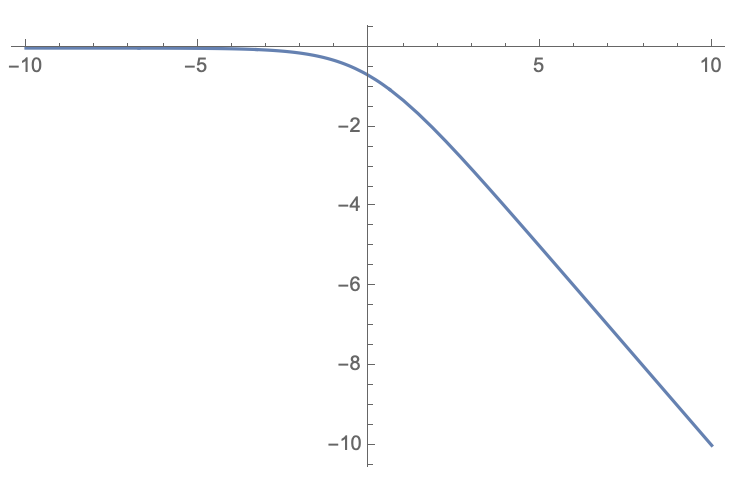
可以看出, x特别小时, 对应的梯度也特别小
式(2)变为:
对应图像为:
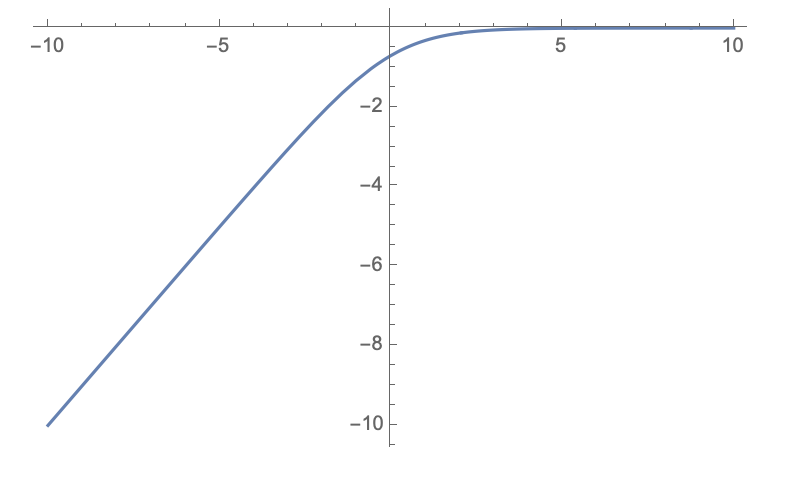
可以看出, x特别小时, 对应梯度很大, 因此generator得到的梯度也很大, 可以加快训练速度